Poughkeepsie, New York
I think there was an error in the reasoning behind my earlier estimate of the force required to insert a device into the Horizon Deepwater well. The actual force required is much less, and it depends on knowing the rate at which the oil is flowing up the well.
Last week I made a rough estimate of the force required to stop the flow of oil out of the Horizon Deepwater well: 1040 tons. I also worked out the rough size of a device capable of withstanding that force, to be slipped into the borehole and then opened up, and from that size estimate I computed the force required to insert the device into the borehole. I said it would take 120 tons for a 10 inch diameter, or "only" 42 tons if the diameter could be reduced down to 6 inches. But I now think that my initial estimate of the insertion force is in error. Here's why, in a somewhat roundabout way:
After I worked out the insertion force, I was wondering how a force of 100 tons (or 42 tons) compares to the capabilities of the equipment BP has available, or what is common generally in the undersea oil industry? I had nothing to compare it to. I also wanted to consider the possibility of replacing the pusher rod with something else that might provide the same magnitude of force. So I searched for information about torpedo propulsion systems. Maybe a torpedo motor could replace the pusher rod? Or in the least it would give something nautical for proper comparison.
I found out that the heavyweight torpedo of the US Navy is the Mark 48. Officially, the top speed of the Mark 48 is reported[1] to be "greater than 28 knots", but unofficially it is estimated to be 55 knots. The diameter of the Mark 48 is 21 inches. From these two numbers we can estimate the maximum thrust of the torpedo. The reasoning is simple: at maximum speed the drag force backward is equal to the thrust forward, and we have all the information needed to compute the drag force on the torpedo.
The drag force of an object moving through fluid depends on the density of the fluid, the size and shape of the object, and the speed through the fluid, according to this equation:
FD = 1/2 Cd A ρ v2where ρ is the density of the fluid, v is the speed through the fluid, A is the cross-sectional area of the object, and Cd is a geometric factor called the "coefficient of drag". The coefficient of drag would be 1.0 for an infinitely large flat plate, and I happen to remember that it is 0.47 for a sphere. I would expect a torpedo to be streamlined enough that we can estimate that Cd = 0.50.
(Incidentally, it's very easy to derive this formula directly from the conservation of energy. Just compute the work required to bring a column of fluid to complete rest, thus reducing the kinetic energy to zero. But I'll save that for some other time, or let you work it out on your own.)
The density of sea water is[2] about 1024 kg/m, and to convert 55 kts to metric units it helps to know that a nautical mile is 6080 feet, and that there are 3600 seconds in an hour. Putting in the numbers and converting back from metric Newtons of force to tons gives a value of about 5.2 tons. Which means it would take about 8 torpedoes to get 42 tons of force. So it seems that using a torpedo propulsion system would not work.
But something is wrong here. If the torpedo is capable of 55 kts in open water, but still could not move upstream in the oil pipe, then you would expect the fluid flowing out of the pipe to be much faster than 55 kts, and that doesn't sound right. So how fast is the oil coming out of the pipe? That's currently a very interesting question. The low estimate from BP has been 5,000 barrels (bbl) per day. Federal officials were estimating it at between 12,000 bbl and 19,000 bbl per day, though recent speculation is that it could be even higher.
It is straightforward to relate the fluid velocity to the flow rate. Imagine a pipe full of oil with cross section A and length L, which therefore has a volume of V=A × L.
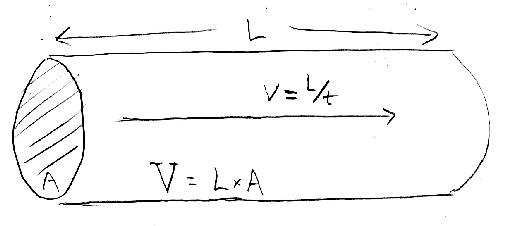
As before, take the diameter of the pipe to be d=21 inches, from which the area can be computed from A=πr2 using r=d/2. The flow rate R needs to be converted to more useful units. It helps to know that one barrel of oil is 42 gallons, which works out[3] to be 0.1589873m3. It may also help to know that there are 86,400 seconds in a day. Then 5,000 bbl/day works out to a fluid velocity of 4.12 cm/s, which less than a tenth of a knot. My baby can crawl faster than that.
Even at a flow rate of 12,000 bbl/day the fluid speed would be 0.2 kts, while at 19,000 bbl/day it would be about 0.3 kts. For 25,000 bbl/day it would be about 0.4 kts. From this we can easily draw two conclusions. First of all, anybody who has seen video of the oil escaping from the pipe (before they put the cap on) can see that the flow rate must have been be well over 5,000 bbl/day. And second, there's no reason that a torpedo with a top speed in excess of 28 kts would not be able to move upstream against this flow (neglecting the tight space of the pipe walls, which is a separate problem). So something is wrong with my initial calculations.
From considering the torpedo example it's pretty easy to see where I went wrong. My original estimate of the force required to hold back the flow was based on multiplying the cross-sectional area of the pipe times 6,000 psi. But that is static pressure, the overall force required to stop the flow completely. Drag force, on the other hand, is dynamic pressure. And it's the drag force that should be applied to anything inserted into the well pipe. The formula above which we applied to the torpedo would also apply to the device inserted into the pipe. This neglects the finite space available for the flow in the pipe, but it's a good first approximation and we can correct for it later. And just as for the torpedo, the drag force increases with the fluid velocity. In fact, it increases like the square of the velocity. Even so, the fluid velocity in the pipe is well below 55 kts (or even 28 kts) and the size of the device is smaller than the torpedo, so the drag force on the device must be well less than the 5 tons of drag force on the torpedo.
So for reference let's use a fluid velocity of 1 knot, which is about 0.5 m/s, (and results in a volume flow rate of about 62,500 bbl/day). Using the density of oil instead of sea water, a diameter of 10 inches, and estimating a drag coefficient of Cd=0.5, I compute the drag force to be 0.70 lbs -- less than a pound.
The drag force goes like v2, so we can easily take the result for 1 knot and multiply by 3025=(55)2 to get the drag force at 55 kts. It works out to be 2132 lbs, or about a ton. Remember, the diameter and density are both less, so we'd expect it to be less than 5 tons.
Now before you get too excited, I can already see that an insertion force of one pound is too low an estimate. There are actually two kinds of drag force. The one we've computed above is called inertial drag, and it is dominant at high speeds (given the dependence on the square of velocity). But there is also viscous drag, which increases only linearly with velocity, and depends on the viscosity of the fluid. Compared to water, crude oil is certainly more viscous, so we really should not neglect it. But that's another calculation for another day. Still, I'm guessing that it will turn out to be significantly less than 100 tons, or even 5 tons.
Thinking about the flow rates also suggests why BP is more interested in capturing the oil rather than simply stopping the flow. The current market price for crude oil is around $71 per barrel. At a flow rate of 19,000 bbl/day that works out to a value of $1.3 Million/day. I don't mind if they capture the oil and sell it. They can use the money to help pay for the clean-up (which I'm sure is costing them more than a million dollars a day), but it would be unfortunate if it biased their decisions against options that could stop the flow in a way that results in more damage to the coastline.
| Copyright © 2014 by Spy Hill Research | https://www.Spy-Hill.net/myers/notes/PipeUmbrella2.html | (served by jura.spy-hill.com) | Last modified: 27 October 2014 |